Tag Archives: dip and strike

Plotting a structural contour map

Leave a Reply
Facebooktwitterlinkedininstagram
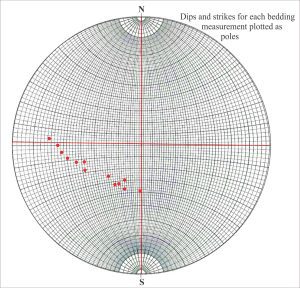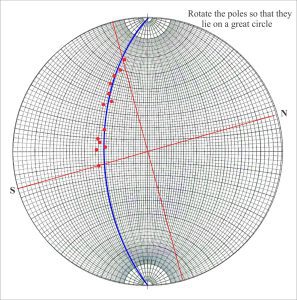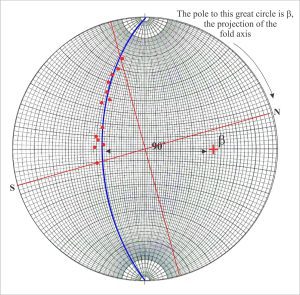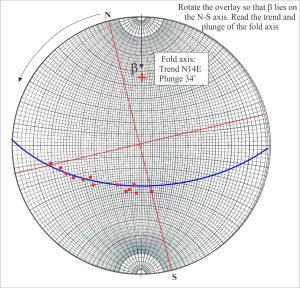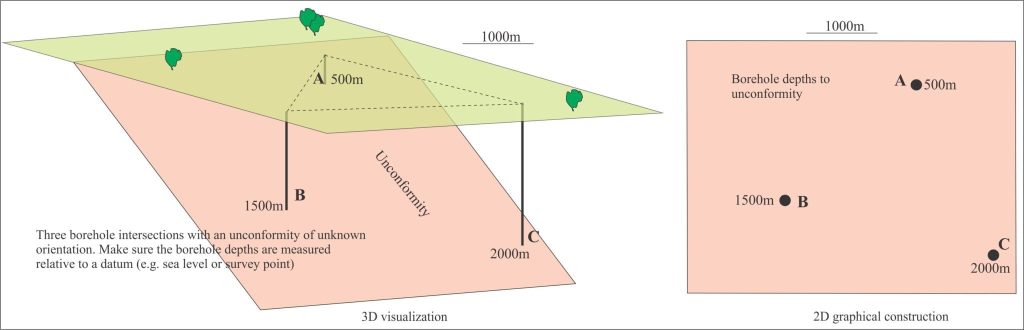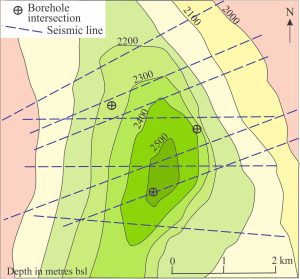
Mapping the structural contours across a stratigraphic unit reveals a three-dimensional picture of its subsurface distribution, deformation, structural relief, and stratigraphic displacement along faults. The structure here is a north-plunging, asymmetric anticline, its eastern limb the steepest. The data needed for this exercise is usually acquired from borehole intersections and velocity-depth conversions from seismic profiles.

Mapping the structural contours across a stratigraphic unit reveals a three-dimensional picture of its subsurface distribution, deformation, structural relief, and stratigraphic displacement along faults. The structure here is a north-plunging, asymmetric anticline, its eastern limb the steepest. The data needed for this exercise is usually acquired from borehole intersections and velocity-depth conversions from seismic profiles.

Structural contour maps are the subsurface equivalent of surface topography maps. They are widely used in exploration geology (regional mapping, hydrocarbons, minerals, groundwater). Frequently mapped surfaces include stratigraphic units, unconformities, basement contacts to sedimentary basins, and igneous intrusive bodies. A completed structural contour map can reveal stratigraphic distribution, structures such as folds and faults, including fault displacement, and paleotopography.

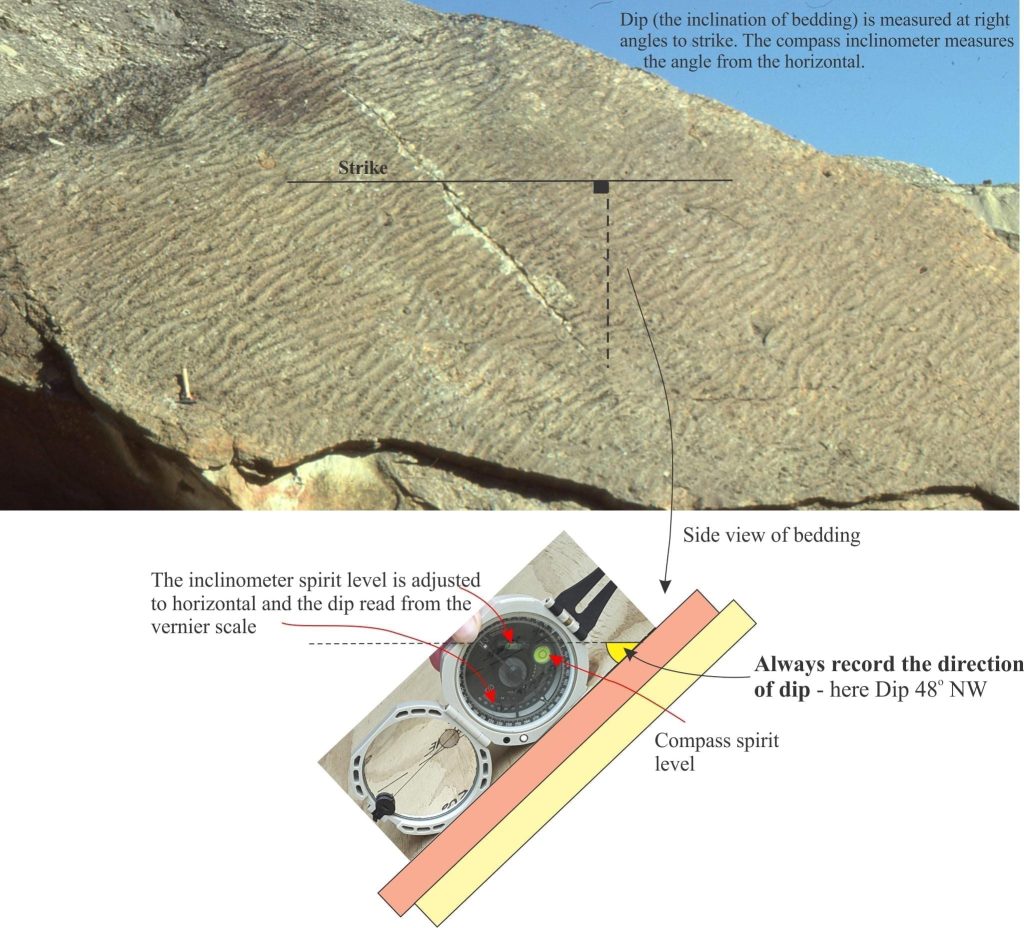
A structural contour is a line of equal elevation across a geological surface. The fundamental difference between structural and topography maps is that the former map surfaces are unseen – beneath the surface. There is also an important difference in the number of data points available for map plotting – there is an almost endless supply of position points for surface topography, particularly in light of advanced satellite imagery and GPS. Contrast this with the small subsurface database that relies primarily on borehole intersections and seismic reflections that require conversion of seismic velocities to depths. Interpolating contours between such widely spaced elevation points requires a decent amount of ingenuity and common sense.

The general rules governing the construction structure contours parrot those for topography plots:

  1. A contour line must remain at its designated elevation.
  2. The elevation interval between contours must be consistent across a map.
  3. Contour lines must never cross or touch one another although they may be very closely spaced.
  4. Contours must never end abruptly except at a map boundary.

Structure contour maps are used widely in surface geological mapping because they provide basic information on outcrop patterns, subsurface extent and structure. The three examples worked through here take the simple case of mapping the geological contacts of a flat sandstone unit. Incomplete sections of the sandstone crop out at two locations: the top at one location at 220 m (above sea level – asl), the base at a second location close by at 200 m asl.

 

A horizontal bed

In this case, the top and base everywhere will be at an elevation of 220 m and 200 m respectively. True thickness is 20 m and we assume this applies across the map area (until we have information that tells us otherwise). In this case, the structural contours coincide with the relevant topographic contours.

 

Geological maps of a flat sandstone bed for the simplest case of a horizontal unit (left) where contacts coincide with topographic contours, and a vertical unit where the contacts cross all contours.

Geological maps of a flat sandstone bed for the simplest case of a horizontal unit (left) where contacts coincide with topographic contours, and a vertical unit where the contacts cross all contours.

A vertical bed

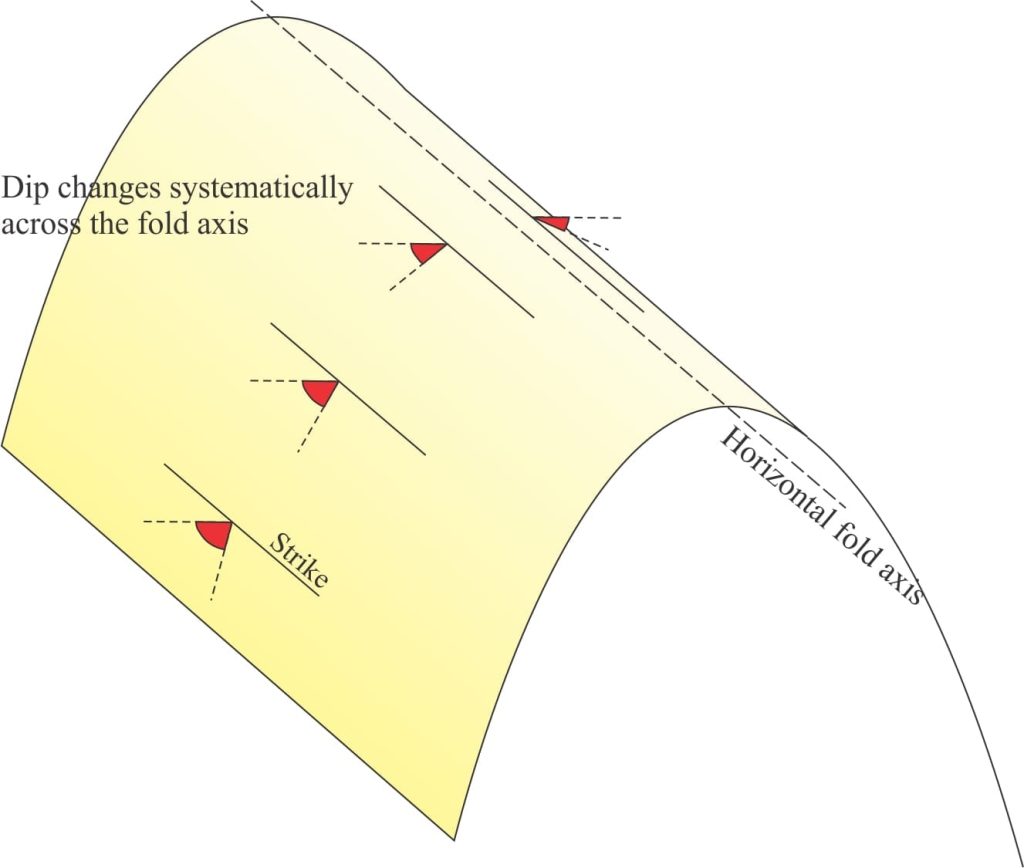
The outcrop trace of a vertically dipping sandstone unit intersects all topographic contours along its line of strike (in this case strike is NE). If the unit is flat, the map extent of the top and base will plot as straight lines. The structural contours in this case correspond to lines of strike. If the unit is folded (and plunges vertically), then the map trace will correspond to a cross-section profile of the fold.

 

A dipping bed

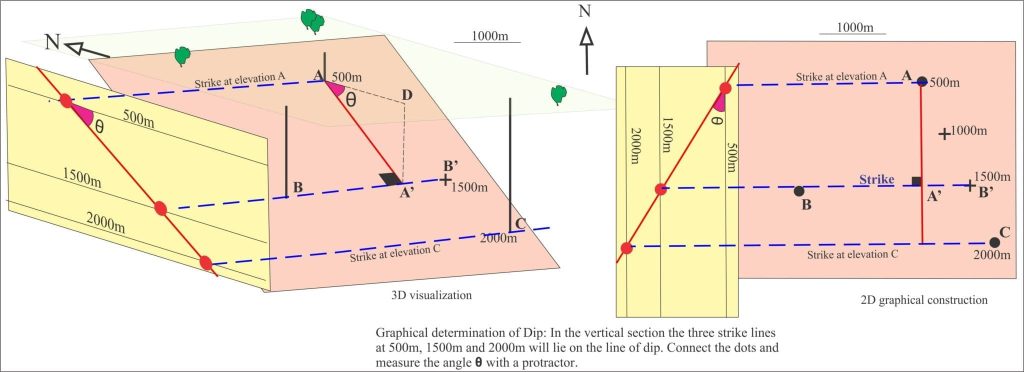
In this scenario, the sandstone unit strikes 045o and dips 25o NW. The structural contours  correspond to lines of strike. What is its map extent?

Because the unit is inclined, the 20 m thickness we determine from the two outcrops must be an apparent thickness. True thickness is calculated as shown in the diagram below.

We need to determine where this dipping unit intersects the surface topography. Beginning with the location where the top is exposed, plot the strike line (everywhere along this line will be 220 m asl), and note where the line intersects the 220 m topography contours at other locations (dashed blue line and dots in the diagram below).

 

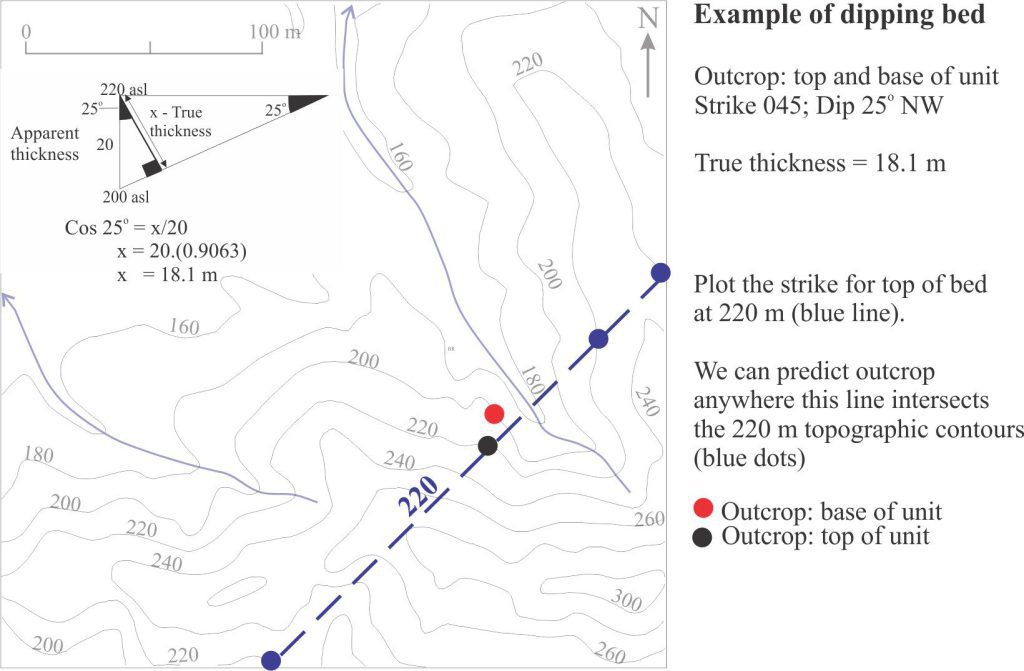
Plotting the strike line for the upper contact of the sandstone and points of intersection between the line and topographic contours of equal elevation.

Plotting the strike line for the upper contact of the sandstone and points of intersection between the line and topographic contours of equal elevation.

Strike lines having the same orientation are now plotted above and below 220 m at elevation intervals corresponding to the topographic contour interval (20 m). To do this we need to calculate the map distance between successive lines given the dip and vertical separation of 20 m. This is shown below (using basic trigonometry functions).

 

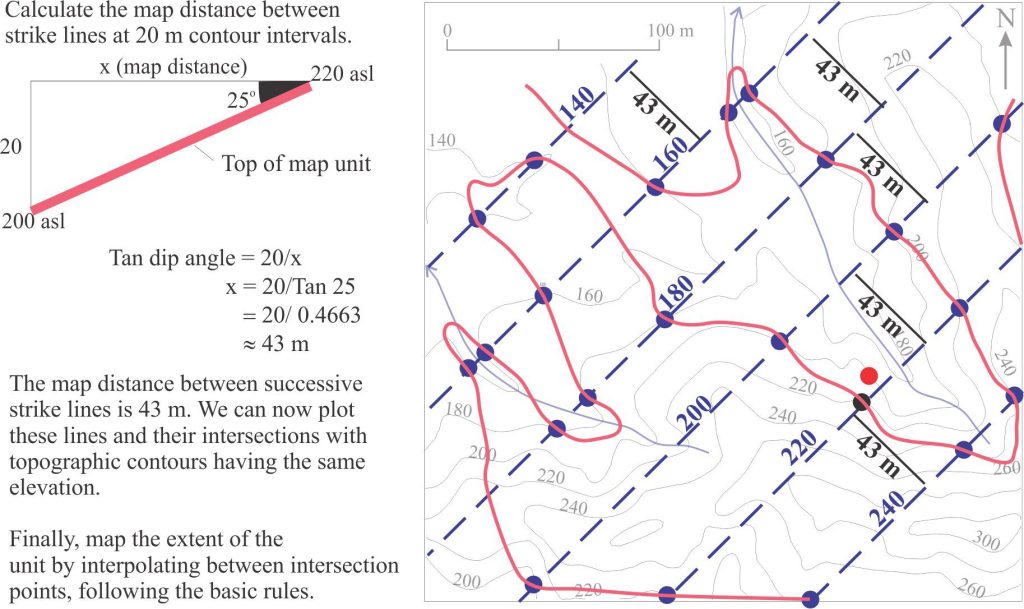
Calculating the distance between strike lines on the dipping, upper contact of the sandstone, plotting those lines and their points of intersection with topographic contours of equal elevation.

Calculating the distance between strike lines on the dipping, upper contact of the sandstone, plotting those lines and their points of intersection with topographic contours of equal elevation.

Strike lines and their intersections with the appropriate topographic contours for the top of the sandstone can now be plotted across the extent of the map. Joining the dots gives us the trace for the top across the map area, taking note of the following rules of interpolation:

  • The trace should never cross itself.
  • The trace can only intersect topographic contours where they have the same elevation (i.e., at the blue and green dots)

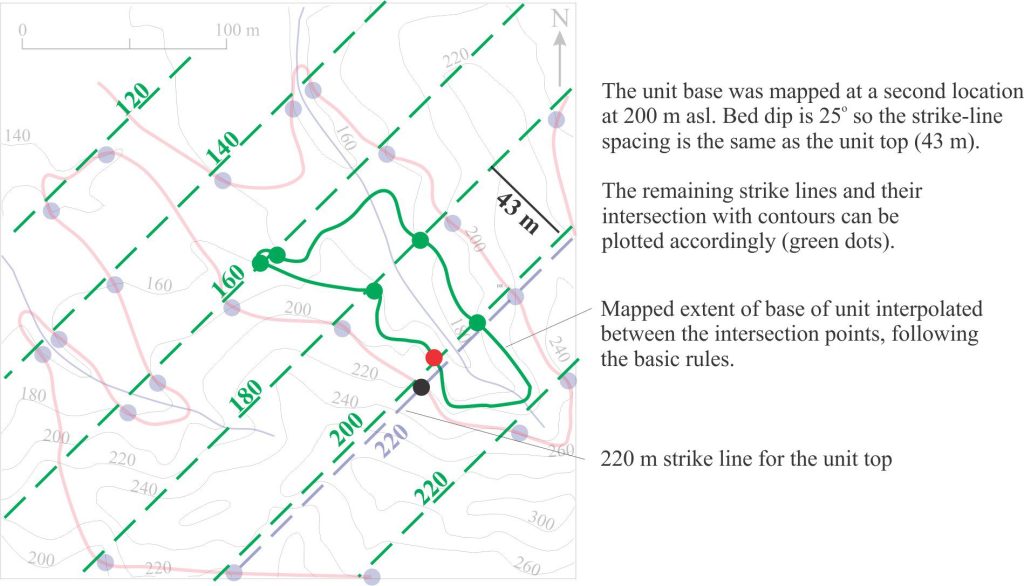
The exercise is repeated for the base of the unit. The map distance (43 m) between strike lines will be the same as that for the top of the unit because the dip is the same. In this exercise, the base of the sandstone is mapped over a small area.

 

Plotting the strike lines and topographic intersections for the base of the sandstone.

Plotting the strike lines and topographic intersections for the base of the sandstone.

Combining the two plots shows the geological map contacts of the sandstone unit. Outside these boundaries the unit either ‘disappears’ beneath elevated topography or has been removed by erosion as is the case for the area enclosed by the basal contact. This is illustrated in the cross-section below; the orientation-location of any cross-section is commonly chosen where it incorporates the most information.

 

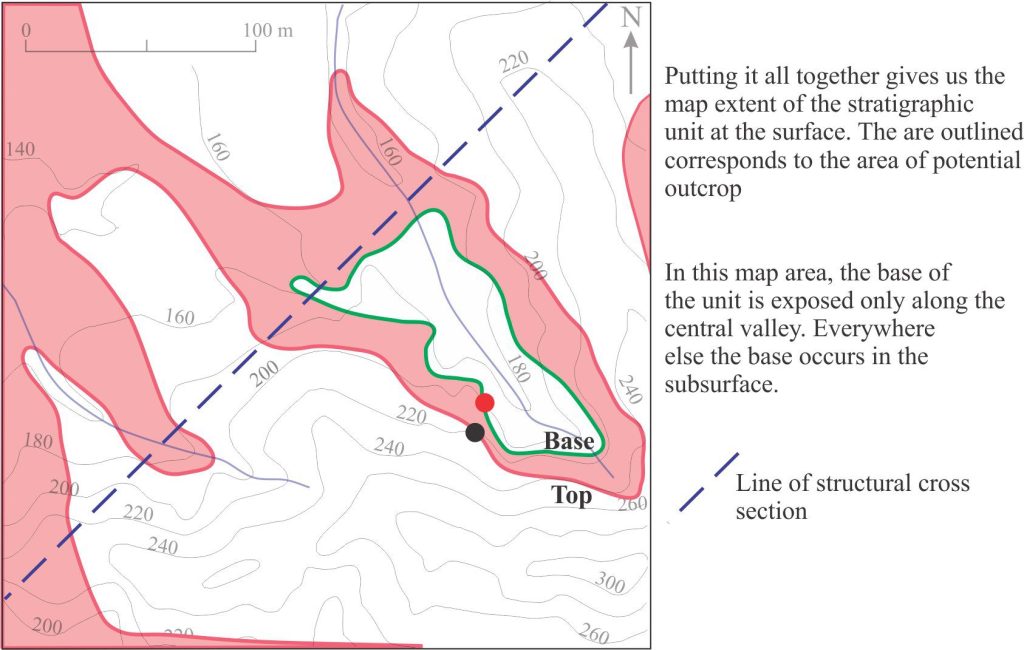
The resulting geological map extent of the sandstone unit, showing where the top and base are expected o crop out. The blue line indicates the location of a structural cross section.

The resulting geological map extent of the sandstone unit, showing where the top and base are expected o crop out. The blue line indicates the location of a structural cross section; it coincides with the 180 m strike line for the top of the sandstone unit.

 

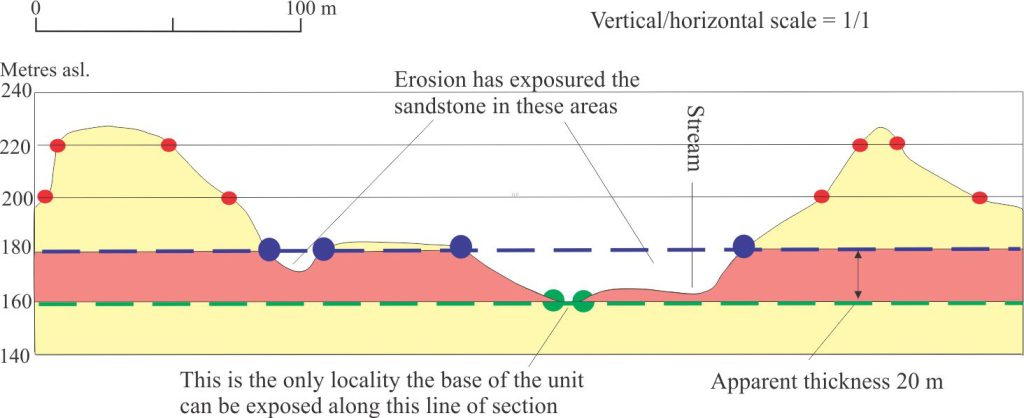
The cross-section (true scale) plots the intersection of strike lines at 180 m (blue dots - top of unit) and 160 m (green dots – base of unit) with topography (red dots). The section locates areas of (potential) exposure. Along this line of section, the map unit base is exposed only in one small area.

The cross-section (true scale) plots the intersection of strike lines at 180 m (blue dots – top of unit) and 160 m (green dots – base of unit) with topography (red dots). The section locates areas of (potential) exposure. Along this line of section, the map unit base is exposed only in one small area.

The cross-section is oriented along the 180 m strike line for the top of the sandstone and drawn at a scale of 1/1 (i.e., there is no vertical exaggeration). It shows:

  • Topography, including stream beds.
  • Because the section is vertical (and the unit has dip), the apparent vertical thickness of 20 m must be shown (not the true thickness).
  • Areas of surface exposure – actual exposure may be limited by covering vegetation, swamps, soils and regoliths, or scree.

Some other posts from this series

Measuring dip and strike

Solving the three-point problem

The Rule of Vs in geological mapping

Folded rock; some terminology

Faults – some common terminology

Thrust faults: Some common terminology

Strike-slip faults: Some terminology

Facebooktwitterlinkedininstagram
Facebooktwitterlinkedin

Stereographic projection – poles to planes

Leave a Reply
Facebooktwitterlinkedininstagram

great circles

 

This post is part of the How to… series

Stereographic projection is used in geology to decipher the complexities of deformed rock by looking at the relationships between planes and linear structures; their bearings (trends) and angular relationships one with the other. The data is plotted on a stereonet as great circles and points (Wulff and Schmidt nets). A stereonet can become pretty messy where there is a lot of data – a seemingly impenetrable maze of great circles. This is where poles-to-planes come into their own.

Instead of plotting the great circle to a planar structure like bedding, we plot its pole. Imagine this as a pole oriented at right angles to the plane. Because the pole is a linear feature, it plots as a point on our stereonet. As long as the pole is 90o to strike, it will contain all of the information in the associated great circle. We refer to this point as the pole to bedding (or any other planar feature). Poles to horizontal planes will plot at the centre of the stereonet; poles to vertically dipping planes at the perimeter. Poles to planes dipping at any other angle will plot within these bounds.

Imagine a pole to oriented normal to bedding. The point of intersection on a great circle contains all the information about the attitude of the bed

Imagine a pole to oriented normal to bedding. The point of intersection on a great circle contains all the information about the attitude of the bed

In the example below the orientation of a bedding plane is plotted on an overlay as a great circle. With the great circle pinned to N, count 90 along the W-E axis passing through the centre of the stereonet; this point is the pole.

Plotting poles to bedding no a stereonet

 

For cylindrical folds the poles to bedding on each limb will all plot on the same great circle (or close to it). The pole to this great circle corresponds to the β point – the fold axis, from which we can read its trend and plunge. Stereographic plots that use poles to bedding or other planes are called pi (π) plots. The utility of pi plots is illustrated in the example of an overturned anticline (the diagrams have been modified from D.M. Ragan, Structural Geology: An introduction of graphical techniques 1968, Figure 11.3).

map of overturned anticline with plotted dips and strikes that can be used to determine the orientation of the axial plane

Dip and strike data on each fold limb are plotted as poles to bedding. We can also locate on the geological map the hinge points for each layer. The line connecting hinge points must lie on the axial surface. However, because our map view is horizontal, this line corresponds to the strike of the axial surface – another important piece of information. What we do not know about this structure is the orientation of the fold axis and the dip of the axial plane. The sequence of diagrams that follows shows the main tasks involved in solving this problem.

  • Find the great circle describing the poles to bedding by rotating a transparent overlay (make sure you mark the original N-S positions on the overlay).

Dip and strike for each measurement plotted as poles to bedding                The poles for each bed dip and strike in the fold lie on a great circle

  • With the great circle pinned to North, count 90o from the circle along the east-west axis (the count must pass through the centre of the stereonet); this point is β, the fold axis.
  • Rotate the overlay counter-clockwise until β lies on the N-S axis. From North, read the fold axis trend and plunge.

                Stereographic determination of plunge and trend of the fold axis

 

 

Stereographic determination of plunge and trend of the fold axis

  • Plot the line representing the strike of the axial surface (N45W). The great circle containing this line must also pass through β.
  • With the second great circle pinned to North, read the dip of the axial surface.
  • Rotate the completed stereonet back to its original position.
The final plot of fold axis and dip of the axial plane

The final plot of fold axis and dip of the axial plane

You now have all the information you need to describe the orientation of the anticline.

Some other posts in this series:

Measuring dip and strike

Stereographic projection – the basics

Stereographic projection – unfolding folds

Using S and Z folds to decipher large-scale structures

Facebooktwitterlinkedininstagram
Facebooktwitterlinkedin

Using S and Z folds to decipher large-scale structures

Leave a Reply
Facebooktwitterlinkedininstagram

Parasitic S-folds in Precambrian mudrocks

This post is part of the How to… series

A problem frequently encountered when mapping structurally deformed rocks is deciding whether the fold you see in outcrop is part of a larger structure – an anticline or syncline, overturned or recumbent, plunging? The problem is exacerbated if stratigraphic facing (younging) criteria are absent or ambiguous. Fortunately, there is a solution to the problem based on fold asymmetry.

Large folds commonly have smaller-scale folds in their limbs and crest. They are usually referred to as higher-order (2nd, 3rd order etc.) or parasitic folds. They form during flexure of layered rock where slip occurs between rock layers – a mechanism called flexural slip. Structural geology teachers frequently use a soft-cover book to demonstrate this mechanism; bend the book into a fold and watch the slip between adjacent pages that is required to accommodate extension on the outer arc of the fold and shortening on the inner arc.

 

Parasitic folds are common in deformed sedimentary rocks where slip takes place along bedding planes or between layers with contrasting strength, such as mudstone and indurated sandstone (mudrocks have abundant clays and micas that are prone to slip and shear). The example below shows an anticline (1st-order structure) and smaller 2nd-order folds developed in a relatively weak layer. The 2nd-order folds have asymmetries related to the sense of slip on each fold limb and are called S- and Z-folds. Note that the 2nd-order M-folds in the hinge are symmetrical and in this example, upright.

Description of s and z folds in an upright anticline

The difference between S- and Z-folds lies in their sense of rotation, or vergence. The long limbs of S-folds are connected by a shorter limb that implies counter-clockwise rotation or sense of displacement; the opposite applies to Z-folds. Thus, the vergence of parasitic folds is towards the hinge line (or zone)

Parasitic Z-folds in banded iron formation; vergence to the right.

 

 

Parasitic S-folds on the steep-dipping limb of an isoclinal fold, in Dalradian psammites, Portsoy, Scotland

 

S- and Z-folds are three dimensional structures and will have hinge lines (or fold axes if we consider them to be cylindrical folds) and axial surfaces that can be measured. Another important property of parasitic folds is that their hinge lines (or fold axes) are parallel (or approximately so) to the hinge line of the 1st-order fold.

A note of caution; the sense of fold rotation-displacement will change if a fold is viewed from the opposite direction (i.e. S-folds will appear as Z-folds). Hence it is necessary to indicate the direction in which observations are made. Where possible, folds should be viewed down-plunge.

The geometric disposition of S- and Z-folds is extremely useful for deciphering large-scale folds, particularly when exposure is incomplete (as is commonly the case). The diagram below shows a scenario, where small folds are exposed in two outcrops.

Deciphering large scale fold geometry from S- and Z-folds

Our view indicates the left outcrop is a Z-fold; the one on the right an S-fold. We can also determine the general attitude of the 1st-order fold limbs from dips and strikes on associated beds. If 1st-order fold-closure is beneath the surface, then it is a syncline (or synform if we don’t know facing direction); if above, an anticline or antiform. Both parasitic folds indicate vergence above the outcrops. If the structure was a syncline then the vergence should be in the opposite direction. The structure is therefore an antiform. If we have good facing direction data we could confirm the 1st-order structure is an overturned anticline (stratigraphy in the right outcrop is overturned).

Some other posts in this series:

Measuring dip and strike

Stereographic projection – the basics

Stereographic projection – unfolding folds

Stereographic projection – poles to planes

Faults – some common terminology

 

Facebooktwitterlinkedininstagram
Facebooktwitterlinkedin

Stereographic projection – unfolding folds

Leave a Reply
Facebooktwitterlinkedininstagram

Restoring paleocurrent trends to their pre-deformation orientations

This post is part of the How To… series

Dipping bedding that is part of a fold limb

Sedimentary strata are commonly deformed. If we assume that the original depositional dip was close to horizontal (this is a reasonable assumption, although there are exceptions) then we need to account for structural dip. This is important if our sedimentary analysis includes measurement of paleocurrents, depositional dip and strike (e.g. ancient shorelines, rivers), or any paleogeographic determination.

Two methods are outlined here: the standard stereographic projection method that is usually done back in the lab unless you are lucky enough to have access to the internet in the field; and a quick field method using a field note book, pencil and compass; this method can only be used in strata folded by a single phase of deformation.

Stereographic method

In the simplest case (diagrams below), strata containing flute casts have been folded into a syncline with a horizontal fold axis; we need to correct the for dip in the fold limb to find the original orientation of the flute cast.   Bedding strikes 080o (N80E), dip 40oN; the flute cast plunges 38o at 315o (N45W).

To determine the original orientation of flute casts, we plot bedding, then unfold the bed on a stereonet

On a transparent overlay, plot the plane (strike and dip) and the line (orientation and plunge) representing the flute cast (it will be a point on the great circle) on the stereonet. To return the plane to its original pre-fold orientation, it must be rotated about its strike; the next step is to move the great circle back to its original plotting position. When the plane is rotated to horizontal all points on the great circle will move along small circles to the stereonet perimeter. The point representing the flute cast is now in its original orientation – here 332o, or N28W. The difference between the uncorrected and corrected bearing is 14o.

Plotting the flute cast plunge and azimuth - it must lie on the the great circle that is bedding

 

 

Returning the dipping bed to its original horizontal position to read the orientation of the flute cast

 

Direct field method

You can use this method when sedimentary structures (or any linear trend) are exposed on bedding planes.  It basically performs the same task as a stereonet correction.

A simple field method to correct paleocurrent dirextions for dip

Place a hard, flat surface on bedding – hard-cover note book or board are good – with the long edge oriented along strike. Place a pencil or similar straight-edge on the surface such that it is aligned with the structure of interest (flute long axis, ripple trend etc). Rotate the book about its long edge (i.e. about the strike) until it is horizontal – make sure the straight-edge doesn’t move. Holding the book and straight-edge in place, measure the bearing.

 

 

If you are not convinced about the accuracy of the field method, check it against the stereonet correction. You will find with practice, and not a little care, that direct field measurement provides excellent results.

 

Some other posts in this series:

Measuring dip and strike

Solving the three-point problem

Stereographic projection – the basics

The Rule of Vs in geological mapping

Folded rock; some terminology

Facebooktwitterlinkedininstagram
Facebooktwitterlinkedin

Stereographic projection – the basics

Leave a Reply
Facebooktwitterlinkedininstagram

Plotting the orientation of a plane on a stereonet; finding strike and dip from two apparent dips

This post is part of the How To… series

 

stereographic projection of lower hemisphere

 

My first exposure to stereographic projection methods of structural analysis was one of my more baffling moments of undergraduate geological learning. Looking around the class I could see I wasn’t the only one. Our tutor, a master at pointing out the obvious, suggested we try thinking in three dimensions. In retrospect it was probably some of the best advice I ever received. After all, geology is nothing if not an exercise in visualizing the 3- and 4-dimensional world around us.

Visualize a sphere; cut the top half off – we don’t need it. If you look directly down the vertical axis of the hemisphere it will appear to be two-dimensional. When you do this, you are basically projecting the 3-D hemisphere onto a 2-D circle. Once this projection has become embedded in your mind’s eye, everything else will fall into place.

The brief animation below shows a hemisphere rotated from an initial oblique view to the point where you are looking directly down the axis (or radius). At this point the hemisphere is projected as a circle that can then be overlaid by a stereonet grid like the example shown above. Each point and curve on the grid represents a point and curve on the hemisphere.

 

 

 

Stereographic projection is all about representing planes (e.g. bedding, foliation, faults, crystal faces) and lines (e.g. dip and plunge directions, fold axes, lineations) onto the 2-D circle. In geology, we overlay the 2-D projection with a grid of meridians, or great circles (analogous to longitudes), and parallels or small circles (analogous to latitudes). Thus, all compass points are represented. The net-like grid is called a Wulff Net, or stereonet. It is an equal angle grid where meridians and parallels intersect at right angles.

plotting a plane on a steronet

 

Note the two extreme projection conditions: the circumference is actually the great circle of a horizontal plane; the opposite is a straight line passing through the centre that is the projection of a vertically dipping plane.  Thus, shallowing dips tend toward the circumference.

The following animation shows how the great circle changes as the plane rotates from vertical to horizontal dip (in increments of 15°). The great circle corresponding to the dip is in red. The line drawn from the two points on the circumference through the centre is the strike.

 

 

In practice we use a transparent overlay pinned to the centre of the stereonet; we rotate the overlay according to the orientation of lines and planes.

Plotting a dipping plane

Follow the next exercise with the short animation. It was made from still images: use the pause and play buttons as you work through the exercise.

 

 

Imagine a plane striking 060o (N60E), dipping 60o SE; the plane passes through the centre of the sphere. In our vertical 2-D view the intersection of the plane with the hemisphere appears as a curved line, or great circle. Rotate the overlay counter-clockwise 60o; mark this point on the circumference. The great circle representing the angle of dip is found by counting along a line at right angles to the strike, i.e. along the E-W axis, counting 60o from the horizontal (the circumference).

Note that in the 2-D view, the great circle meets the circumference at 060o and 240o that are two points on a horizontal line across the plane; the great circle is therefore the strike of the plane.

If a plane projects onto the stereonet as a great circle, then a line or lineation on the plane will plot as a point on the same great circle. To illustrate, we will find the true dip and strike of a plane for which we have measured two apparent dips: (1) 30o at 315o (N45W) and (2) 32o at 014o (N14E). On a transparent overlay, mark the positions of the N-S and E-W axes, and the stereonet centre. For (1), rotate the overlay 45o clockwise, mark the position at the N pole, then count 30o from N along the N-S axis. This point is the projection of apparent dip (1). Likewise, repeat for apparent dip (2). Rotate the overlay until the two apparent dip projections lie on the same great circle – read the bearing from N and the true dip along the E-W axis.

 

Determining apparent dip on a stereonet

Follow this exercise with the short animation. It was made from still images: use the pause and play buttons as you work through the exercise.

 

 

Stereographic projection is a powerful method, not just to solve relatively simple (but important) problems of dip and strike, but as an analytical tool for more complex structural geology. There are several good software programs and Apps to automate projections for large data sets. But before you dive into these digital tools, try the simple overlay first – there’s nothing like a hands-on approach to help galvanise an understanding of basic methodology.

Some other useful posts in this series:

Measuring dip and strike

Solving the three-point problem

Stereographic projection – unfolding folds

Stereographic projection – poles to planes

The Rule of Vs in geological mapping

Folded rock; some terminology

Here are some good website links:

Visible Geology

Rick Allmendinger’s Stereo 10 – there’s also a mobile App version

Innstereo (open source)

Links to several programs in The Structural Geology Page

Facebooktwitterlinkedininstagram
Facebooktwitterlinkedin

Solving the three-point problem

Leave a Reply
Facebooktwitterlinkedininstagram

A graphical method for solving the three-point problem

This post is part of the How To… series

Determining the orientation of a plane given the points for three intersecting wells.

Determining the orientation of a plane given the points for three intersecting wells.

Mapping is the essence of geology. Geology maps provide the wherewithal to decipher the time and space organization of Earth’s solid and fluid spheres. We map the outer veneer by directly observing rocks and fluids, ‘walking out’ rock units, measuring, sampling and imaging as we go. More recent tools include all manner of remotely sensed data and satellite imagery (seismic, Lidar, radar, Landsat). We apply the same tools to map other planetary surfaces, although the walking-out is done by remotely controlled rovers.

Subsurface mapping is the essence of all explorations for aquifers, hydrocarbons, minerals, geothermal energy and geotechnical constructions. Subsurface mapping provides us with a deeper (sic) understanding of how the Earth works. Subsurface mapping is entirely dependent on remote sensing (e.g. seismic, gravity, radar) and borehole probing.

The orientation of geological planes in the subsurface is no less important than in surface mapping, but the database is commonly one-dimensional (e.g. borehole depths and lithologies). For example, a zone of mineralization at depth lies beneath an unconformity; knowing the orientation of the unconformity plane will give us more confidence predicting the trend of mineralization (assuming the unconformity is reasonably flat). To solve the problem, we need depths from three borehole intersections with the plane. The solution is commonly referred to as the 3-point problem. It is based on an understanding of dip and strike.

 

Geometric calculation of dip and strike in a 3-point problem

Geometric calculation of dip and strike in a 3-point problem

A graphical solution is shown in the animation. You need paper, a ruler and a protractor. This method requires the horizontal and vertical (depth or elevation) scales to be the same (no vertical exaggeration). Normally the construction would be done on the plane itself (i.e. 2-dimensional) – here the 3-dimensional view has been added to help you visualize the problem.

The animation was made from still images: use the pause and play buttons as you work through the exercise.

 

Some other useful posts in this series:

Measuring dip and strike

Stereographic projection – the basics

Stereographic projection – unfolding folds

The Rule of Vs in geological mapping

Folded rock; some terminology

Facebooktwitterlinkedininstagram
Facebooktwitterlinkedin

Measuring dip and strike

1 Reply
Facebooktwitterlinkedininstagram

How to measure dip and strike

This post is part of the How To… series

If we had to designate one set of measurements that is fundamental to all geology, it would have to be Dip and Strike. These simple measures define uniquely the orientation (compass bearings and angles) of a planar surface – any plane: bedding, faults, axial planes, mineralized veins, dykes and sills. Armed with dips and strikes, a geologist can project planes and the rocks they encompass across valleys, through mountains and deep beneath the Earth’s surface.  They are fundamental to deciphering Earth structures.

Strike: The compass bearing of an imagined horizontal line across a plane. If the plane is flat there is an infinite number of strike lines, all having the same dip (zero) but different bearings. If the plane is curved (e.g. a plunging fold) the bearing may change systematically over the fold.

Azimuth, or compass bearing is recorded as either (for example) 035o or N35E, or its counterpart 215o and S35W.

Visual description of dip and strike on bedding.

Dip: Dip is the angle of inclination measured from a horizontal line at right angles to strike. The angle is measured by placing a compass on the line of dip and rotating the inclinometer to the point where a spirit level indicates horizontal. The direction of dip need not be measured (it can be calculated directly from the strike bearing), but an approximate direction should always be recorded to avoid ambiguity, as in 48oNW.

The inclination measured at right angles to strike is the true dip. Inclinations measured at other angles on the plane will always be less than true dip – these are called apparent dips.

The animation below was made from still images: use the pause and play buttons as you work through the exercise.

Dip and strike indicate the orientation of a plane at a specific location.  Dips and strikes of folded strata will tend to show systematic changes at different locations. In the example below the fold axis is horizontal and axial plane vertical. Strikes at any point on the fold limbs will all have the same azimuth, but dips will change progressively from one limb to the other.  Dips and strikes recorded on geological maps can be used to reconstruct the 2- and 3-dimensional structure of deformed strata.

Systematic change in dip through an folded plane; in this example the strike remains the same throughout.

Some other useful posts in this series:

Solving the three-point problem

The Rule of Vs in geological mapping

Plotting a structural contour map

Stereographic projection – the basics

Stereographic projection – unfolding folds

Folded rock; some terminology

Facebooktwitterlinkedininstagram
Facebooktwitterlinkedin